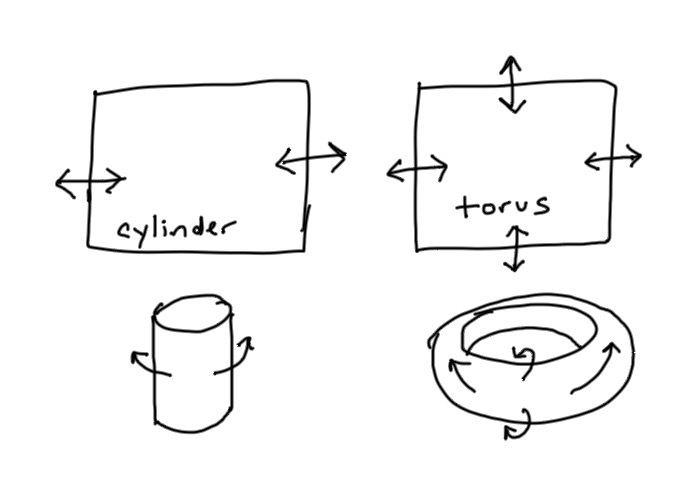
Some games have tile maps that wrap around. Civilization for example lets you go off the left side of the map and you warp to the right side. You can’t go off the top or bottom of the map. In 3D space, this would be a cylinder. Some games also let you go off the top side and warp to the bottom, and vice versa. In 3D space, this would be a torus.
Most wraparound tile map games don’t use a sphere like an actual planet. What are its properties?
- You can walk west/east and wrap around the map. This is like the cylinder or torus.
- You can walk north/south but you do not wrap around to the other side. This is like cylinder but unlike torus.
- You can walk past the north/south poles and stay at that pole but are facing the south/north instead of north/south. This is unlike cylinder or torus.
- Walking west/east to wrap around the map takes less time (shorter distance) near the poles than near the equator. This is unlike cylinder or torus.
Wouldn’t that be cool? Why don’t tile map games use this?
- You can’t tile a sphere with uniform regular square or hexagon tiles (Euler said so![2]). If you try to tile with hexagons (by subdividing an icosahedron), you end up with twelve pentagons left over. In the image on the right it’s easy to spot them, but even in a map with millions of tiles, you will still have those twelve pentagons hiding among millions of hexagons.
- The need for polar regions to be narrower means it has a more complicated coordinate system that doesn’t allow rectangular grid maps.
- The need to flip direction when passing a pole makes camera orientation tricky. You can’t have a camera that’s always facing north. It either needs to rotate freely or it needs to flip upside down when you pass the pole.
So it looks like it may not be practical to flatten a sphere onto a flat grid, but I wanted to explore it anyway. (Note: the /x/ in the url is where I put my quick, unpolished projects like this one.)
The first problem is: what coordinate system should I use to represent the player’s position and direction, in a way that makes walking around the pole shorter than walking around the equator? A common way of tesselating a sphere is to subdivide an icosahedron. (Note: if you want to use square tiles instead of hexagon tiles, unwrap a cube.) That icosahedron, when unfolded, can look like this:
The second problem is: what should I do with those leftover pentagons? They won’t work with a flat tile map. I’m going to try hiding the pentagons by just not letting you walk near them. This would only work in games where you’re walking/driving and not games where you can zoom out or freely control the camera.
The third problem is: what should happen when you pass a pole? I’m going to rotate the camera and make it only let you see the local area.
Idea 1: two-level coordinate system
Treat each region separately. Keep track of which region you are in, and then keep a local x,y coordinate inside of that triangle. When crossing a boundary into another region, calculate the new x,y.
Distances and vectors that cross a region boundary becomes hard. There are no distance or angle distortions for local calculations. Since region crossing is complicated, it’d be best to avoid combat or even land masses crossing regions.
Idea 2: convex coordinate limit
Use a single x,y coordinate for the entire world, but limit it to this shape. If you try to exceed the y bound, you stop at the edge. If you try to exceed the x bound, you wrap around. The triangles are distorted though, especially near the poles.
While global calculations may be a little better, distances and angles are distorted locally. I don’t think this will work well.
Idea 3: teleport regions
Use a single x,y coordinate for the entire world, but limit it to the blue area shape. If you try to exceed the y bound, you stop at the edge. If x goes off the left/right side of a triangle region into a red area, you are teleported into a nearby valid green area region. This doesn’t work near the triple points (where the pentagons are) but if you can’t get close to the pentagons anyway it shouldn’t be a problem. We need to translate both positions and directions to the new triangle.
This is sort of a hybrid of idea 1 (separate regions, two-level coordinate) and 2 (all one region, single coordinate). In the ten tropic regions, it’s all connected; region crossing is easy and acts like a torus. In the ten temperate/polar regions, they’re separate; region crossing requires changing coordinates and directions. Like idea 1, there are no distance or angle distortions for local calculations. The advantage over idea 1 is that you can have larger continents that cross any boundary that includes one tropic region. The advantage over idea 2 is that there are no local distortions.
Flat rendering#
This is what I’ve been working towards: you can drive around (WASD or arrows) and you see a hexagonal grid everywhere, but the underlying behavior is approximately a sphere. You need to stay away from the pentagons; the danger zones are dark gray hexagons. This works on Chrome but not on all browsers. Sorry.
The idea is to adjust triangular regions near the poles to be adjacent to the ones the player is in. Then when the player moves away we’ll adjust them back, out of sight. The area near the player always looks flat as long as you don’t get near the pentagons.
I made the tiles fairly large for this demo but in a real game you could have a much larger map with millions of small hexes, and you’d never get too close to the pentagons. You can’t allow the player to zoom out to keep this working, unless you’re willing to switch to a 3D sphere view when zooming out.
Implementation: determine the region the player is in, then draw that region plus the three adjacent regions. For this demo however I implemented a slightly easier approach: determine the four-region “column” the player is in, and render those four plus the six neighboring regions. I haven’t yet worked out mathematically how far from the pentagons we need to stay but for the demo I just tweaked it until it’s good enough.
There are some bugs in my quick & dirty demo, and some features I wanted to add:
- The areas near pentagons are forbidden zones but the demo lets you drive there.
- It doesn’t work across browsers (for reasons I haven’t figured out).
- The “sphere” should be drawn as a sphere, not an icosahedron.
- The sphere should include the numeric labels and the player’s position.
However I’m not actively pursuing this idea, so I’m not going to spend a lot more time on it right now.
Other projections#
Subdivided icosahedra are the usual shape because they are the most sphere-like, but we can use any of the Platonic solids, or truncated solids, to build a sphere-ish map[3]:
| Solid | Number of sides | Shape of sides | Tiling |
|---|---|---|---|
| Icosahedron | 20 | triangles | triangle, hexagon |
| Dodecahedron | 12 | pentagons | pentagons?[4] |
| Octahedron | 8 | triangles | triangle, hexagon |
| Cube | 6 | squares | square |
| Tetrahedron | 4 | triangles | triangle, square |
The unfolded cube in particular would be the first thing I look at if I wanted square tiles:
The unfolded tetrahedron (1[5], 2[6]) is quite distorted relative to a sphere but in a game that may be ok. The main advantage is that we can use a rectangular coordinate system, if we glue the right half of triangle 3 onto the left half of triangle 0:
- Left/right wraparound is simple: set
x = x % 2. - Top/bottom wraparound is relatively simple too: set
x = 2-xand leaveyalone, and flip the player’s camera to point south instead of north or vice versa. Moving up from triangle 1 leads to triangle 3 and vice versa; moving down from triangle 0 leads to triangle 2 and vice versa.
[2021-Apr] I made an an animated rendering of the tetrahedron approach.
Like the tetrahedron approach, the Peirce quincuncial projection[7] and Guyou hemisphere-in-a-square projection[8] and Adams hemisphere-in-a-square projection[9] also have simple wraparound coordinate systems. See this visualization of Peirce[10] from @mbostock. Both are conformal[11] projections, which preserve angles and local scale.
Octahedra also look promising. See the diagram here[12]. I have not explored this.
If you’re looking for a way to wrap your head around these polyhedra, this page[13] links to some PDFs for tetrahedron, cube, octahedron, icosahedron, dodecahedron, and other maps.
References#
Working on this miniproject, I decided working with spheres was more effort than I wanted to put into a game, unless the sphere was an essential part of the game. What other ways are there to tile a sphere, and also make it easy to work with?
- I first got interested in this when answering this stackoverflow question[14] a few years ago; the visualization from https://github.com/vraid/earthgen-old[15] is beautiful! But it too has pentagons. Also see this stackoverflow question[16].
- This page[17] explains map projections and Tissot’s indicatrix, with interactive diagrams.
- The board game Invasion Earth[18] used an unfolded icosahedron projection.
- Dymaxion map[19] (or “Fuller Projection”) is Buckminster Fuller’s nonuniform unfolding of an icosahedron that fits all of Earth’s continents onto the map without splitting any of them at the discontinuities of the unfolding. To do this, he splits some of the icosahedron triangles into smaller shapes.
- This demo[20] lets you move around on a Dymaxion map; it will show you how the triangles are oriented relative to your position.
- This discussion thread[21] includes a post by “coregames” on page 3 showing a hexagonal tiling of the unfolded icosahedron.
- Tissot’s indicatrix[22] is a visualization of distance, angle, and area distortions caused by a map projection. The “World maps comparing Tissot’s indicatrices on some common projections” section of that page shows how common map projections fare. An unfolded icosahedron seems to do fairly well.
- HEALPix[23] tiles the sphere with equal-area but not equal-shape quadrilaterals. I wonder if we can locally display each of those quadrilaterals as a square tile (and prevent the player from approaching problem areas, just as on this page). → Two years later, I did experimented with this.
- Hexasphere[24] claims to have a hexagonal tiling of the sphere without pentagons. They don’t. (It’s an April 1 page.) Herman Tulleken explains how it works[25] (torus instead of a sphere). There’s also a video[26] with code.
- “What is the best way to pixelize a sphere?”[27] has some math for icosahedron spheres.
- This page[28] compares several approaches for certain types of calculations, but it doesn’t seem especially relevant for games.
- There’s also a way to tile a sphere using the rhombic dodecahedron[29] instead of an icosahedron. It looks like it might work for square tiles, but like the hexagon+pentagons approach, there will be a few places on the map where normal geometry doesn’t hold, so those will have to be treated specially.
- This map projection[30] is based on a tetrahedron instead of an icosahedron. Just as a raw icosahedron map splits the Earth’s continents, and the Fuller projection fixes it, a raw tetrahdron map splits the Earth’s continents, and the Authagraph projection fixes it.
- This site[31] has the most comprehensive list of projections I’ve found, including at least three tetrahedral variants. Also see the Markley projection[32].
- I haven’t read this book but Divided Spheres[33] probably goes into all of these topics in much more detail.
- hexasphere[34] is a Javascript library to create spheres with hexagons + pentagons. There’s also an Objective C port.
- The H3 hexagonal system uses a sphere rotated so that the pentagons are in Earth’s oceans[35], the same as Buckminster Fuller’s Dymaxion map projection.
- FreeCiv has a discussion page[36] about switching from cylinders to spheres.
- I ended up using Voronoi instead of hexagons for a sphere map.
- Before We Leave[37] is a game on a sphere that hides the pentagons under mountains and oceans.
- The GS50 map projection[38] uses 9 discontinuity points outside the map area to make the United States projection work nicely. Although it’s not directly related to this page, it shares the idea of moving the problem areas to places that aren’t of interest.
- A paper came out in 2019[39] (after I had written this page) about how to place the problematic corners (pentagons) to avoid land masses on the Earth. Their algorithm seems like it could work for procedurally genreated worlds too.
- Climate Modeling with Spherical Geodesic Grids[40] [PDF] shows how to store these hexagonal sections in a rectangular grid. They combine 4 triangular areas into a parallelogram and use these regions for fluid simulation.
Followup: I experimented with square tiles on a sphere.
