Breadth First Search: multiple start points

Running Breadth First Search with multiple start points can do some cool things. If you haven’t already read my page about Breadth First Search, that would be the place to start before reading this page. The ideas here are a modification of the algorithm presented there. Note that even though the demos on this page use a square grid, none of these algorithms is limited to only square grids, or even to grids.

Distance to nearest obstacle#

Nairou on StackExchange asked how to calculate the distance to the nearest obstacle^[1] in a single pass. One answer is Breadth First Search. Usually in pathfinding we initialize the open set with a single start point, but when calculating the distance to the nearest obstacle, we consider each obstacle a start point. Here’s a quick & dirty demo. Click to cycle among: open space (blue), start point (purple), and wall (gray)

Here’s some Python code. It’s similar to the code on my page about Breadth First Search, but instead of a single start point, we’ll have many:

frontier = Queue()
cost_so_far = dict()

# Starting points get distance 0
for location in start:
   frontier.put(location)
   cost_so_far[location] = 0

# Expand outwards from existing points
while not frontier.empty():
   current = frontier.get()
   for next in current.neighbors():
      if next not in cost_so_far:
         cost_so_far[next] = cost_so_far[current] + 1
         frontier.put(next)

Distance to nearest intersection#

Here’s a different example using the same algorithm. The Pac-Man Safety Map^[2] tells you the distance to the nearest intersection. Mark the intersections as start points (purple). In this demo I also marked entrances to the big room on the left, but try marking anything you want:

Distance to nearest wall#

Here’s the same algorithm with the walls as the start points. It tells you not only the size of the room but also how to move towards or away from the center. Click to toggle walls:

Walls, intersections, enemies, allies, resources, bosses, treasures — there are so many types of map analysis you might do with this. For example, corridors are 1, but doorways and other tiles have 1 also. If you mark all the tiles that are 1 and are surrounded by 0 or 1, those will be the corridors.

Region growth#

In addition to the distance, we can keep track of which  start point (seed) that distance is based on. We will end up with a map that tells us which start point is closest to each other point based on travel distance. Choose start points:

frontier = Queue()
cost_so_far = dict()
started_at = dict()

# Starting points get distance 0 and
# will point to themselves
for location in start:
   frontier.put(location)
   cost_so_far[location] = 0
   started_at[location] = location

# Expand outwards from existing points
while not frontier.empty():
   current = frontier.get()
   for next in current.neighbors():
      if next not in cost_so_far:
         cost_so_far[next] = cost_so_far[current] + 1
         started_at[next] = started_at[current]
         frontier.put(next)

The distances are calculated in the same pass, and tell you how far any tile is from the start point (capital city maybe), as well as the path to that point:

Run Breadth First Search a second time, this time with the country borders as the start points, and you can find distances from the border, and also paths to the nearest border. The highest distance is the point farthest from a border.

Island Connectivity#

A variant of the previous idea is to traverse the map and use every location as a region start point, if it hasn’t already been assigned to a region. This is called Connected Components^[3] in graph theory. It’s useful in maps to identify islands. We’ll run Breadth First Search from every land point, but won’t allow moving into water. Toggle water/land on the map to see the island labels:

Isn’t that a lot of Breadth First Searches? Yes, in theory. In practice we can do it all in one Breadth First Search where we insert another node into the queue every time it empties. Here’s a rough sketch (but I haven’t tested this code):

frontier = Queue()
started_at = dict()

# Run Breadth First Search to find islands. Instead of stopping
# when the queue is empty, we'll look for a tiles that haven't
# been visited yet, and add it to the queue.
for location in all_land_tiles: # don't include water tiles
   if location in started_at:
      continue  # already assigned to an island, skip it

   # This location is on land but hasn't been assigned to
   # an island yet, so it will become the new island id
   frontier.put(location)
   started_at[location] = location

   while not frontier.empty():
      current = frontier.get()
      for next in current.neighbors(): # exclude water
         if next not in started_at:
            started_at[next] = started_at[current]
            frontier.put(next)

To find distances from the coast, run Breadth First Search a second time, with all land tiles as the start points and allowing movement through water:

During the neighbor loop in Breadth First Search, if the current node and the neighbor node come from two different islands, that’s a potential place for a bridge. You can think of this as a new graph: islands are nodes and potential bridges are edges. The simplest approach (shown in the diagram) would be to connect them all. If you want to connect only some, a Spanning Tree would connect all islands together. A Minimum Spanning Tree would minimize the length of the bridges. There may be many mathematically equally short bridges though, and you may need to add heuristics to choose the bridges that you find most visually appealing.

For the first part (Connected Components) it doesn’t matter if you use Depth First or Breadth First, but since I use Breadth First for so many other things I often use it here too. The above algorithms work for undirected graphs, but if you have a directed graph, it’s a little trickier to decide what a Connected Component is. If your graph is changing over time, there may be update algorithms that work more efficiently than recalculating from scratch, but recalculating is simple. For example, if you only add land tiles, the Union-Find^[4] data structure may be useful.

Combining fields#

The above examples calculate a single distance field to find the closest source, but sometimes it’s useful to calculate multiple distance fields and then combine them. The combined distance field to the closest source is the min() of multiple distance fields. Here’s a demo showing the combination of two distance fields:

Keeping the distance fields separate and using min() allows toggling each source on/off without having to recalculate the combined distance field. Other combination functions such as max, sum, difference, etc.can be used to implement “influence maps” and map analysis^[5] features.

More ideas#

The same algorithm works on a polygon mesh. Switch to Dijkstra’s Algorithm to extend this to work with variable movement costs. Take a look at this article^[6] for more ideas.

There are other algorithms, some of them more easily parallelizable or GPU-friendly than Breadth First Search. See Distance Transform on Wikipedia^[7]. For Euclidean distance instead of Manhattan Distance, see 2D Euclidean Distance Transforms: A Comparative Study^[8] (PDF).

1. In a map generation experiment^[9] I started at the coastlines and used Breadth First Search with some randomness to generate rivers.

   

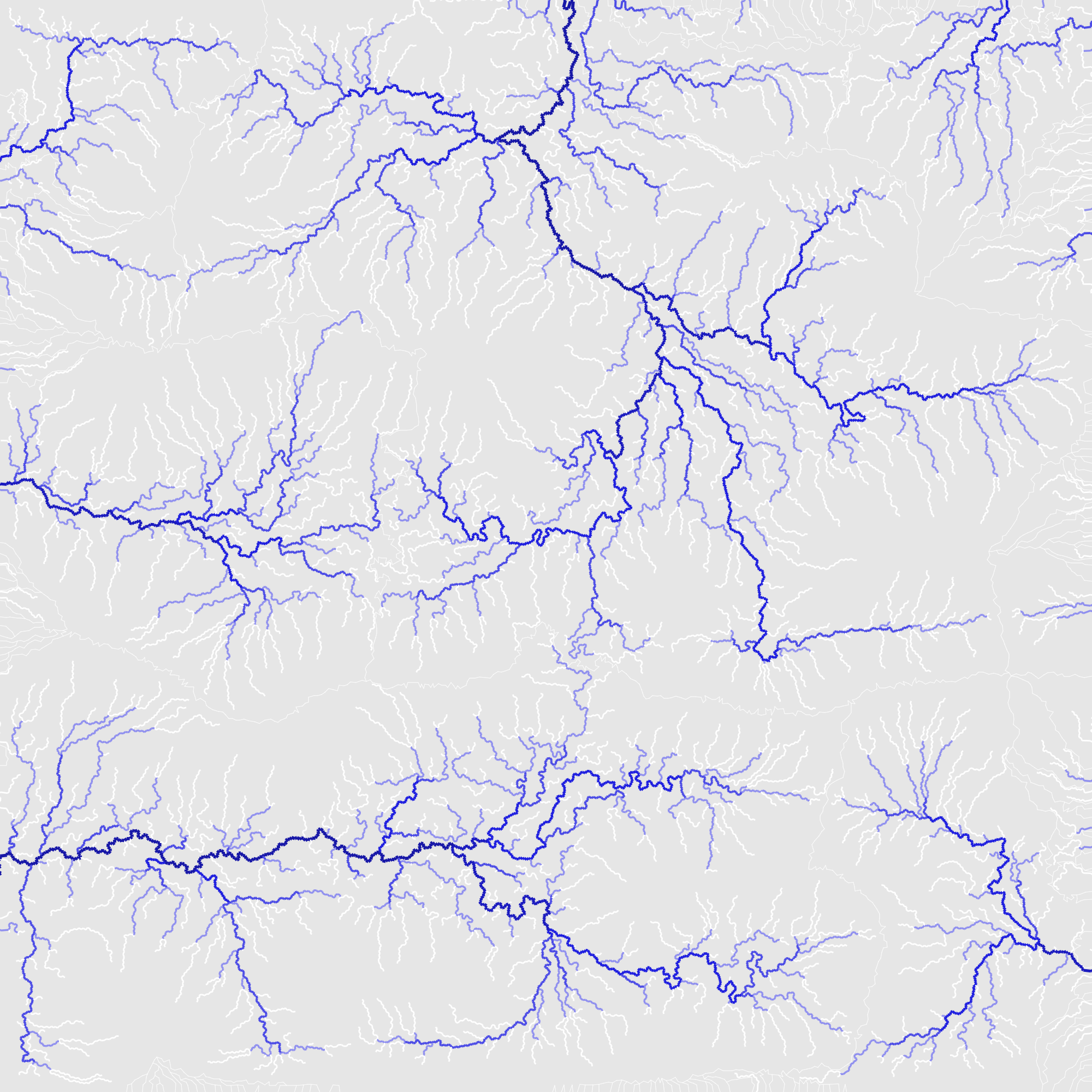
2. In Mapgen4 I used Breadth First Search not only for rivers but also for climate.

   

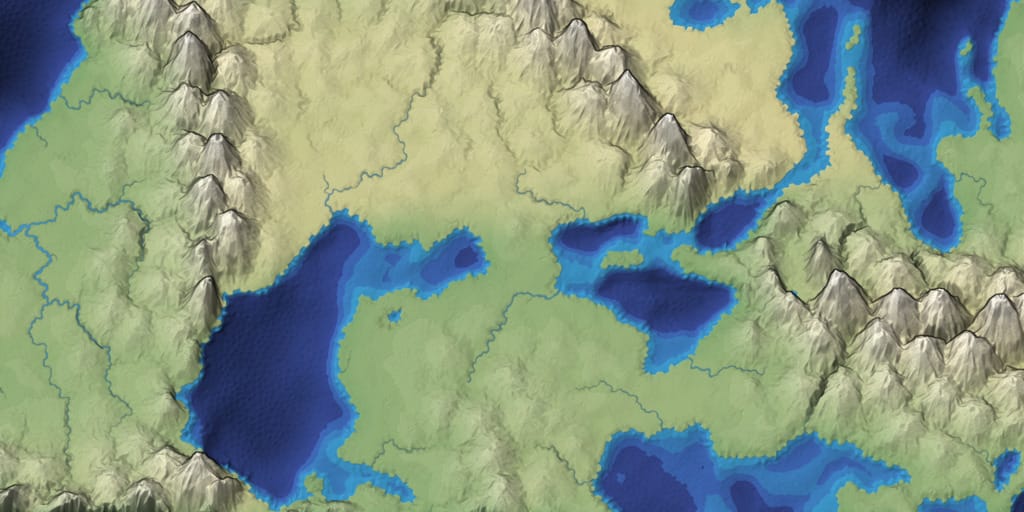
3. In this dungeon generator I ran Breadth First Search serially instead of in parallel across all seeds, and I also put limits on how far it grows. I used this to generate dungeon rooms.

   

Breadth First Search can run at around 1 million nodes per second.