I had previously made a logo generator that generated bitmaps, because I needed bitmaps for use on social media sites. I wanted to make one for the axidraw plotter, but I needed a vector format. Even though I could convert the face generator commands to vector format, I am using clip regions for it, and the plotter doesn’t support clip regions or polygon fills. So I’m making one specifically for the plotter, and I might be able to reuse it for non-plotter applications too.
Or I can generate lots of them:
Instead of using a clip region, I need to clip the teeth to the mouth shape. The mouth shape is in four segments:
I need to take each of the vertical line segments for the teeth and clip it to the mouth shape. I also need to take the horizontal section that doesn’t have teeth and fill it from left to right.
Since these are quadratic bezier curves[1], I think I can solve them directly. The quadratic spline formula usually takes \(t\) as input and outputs a point \(S\):
| \(S =\) | \(\quad \quad (1-t)^{2} * P\) |
| \(+\quad 2(1-t)t * Q\) | |
| \(+\quad t^{2} * R\) |
I want to rearrange this to a polynomial of \(t\):
| \(0 =\) | \(\quad \quad P t^{2}\) | \(- \quad 2 P t\) | \(+\quad P\) |
| \(-\quad 2 Q t^{2}\) | \(+\quad2 Q t\) | ||
| \(+\quad R t^{2}\) | |||
| \(-\quad S\) |
where \(S\) is the target value. So now I can use the quadratic formula[2] to solve this:
\[ t = \frac{-b ± \sqrt{b^{2} - 4ac}}{2a} \]
where \(a = (P - 2*Q + R)\); \(b = -2*P + 2*Q\); \(c = P-S\). Does this work? I’ll try it and see. It didn’t work. But that’s because I had gotten the math rearrangement wrong (forgot a minus sign). Since I had written down all the intermediate steps, I could bisect to find my algebra error and fix it. Now it works. Given \(S\) I can find \(t\).
Note: I also tried the alternate form[3] but it wasn’t any better in this case:
\[ t = \frac{-2c}{b ± \sqrt{b^{2} - 4ac}} \]
When I use the \(x\) values from P, Q, R, I can solve for some desired \(S=x\), to get the clipping range for the horizontal lines. When I use the \(y\) values, I can solve for some desired \(S=y\), to get the clipping range for the vertical lines.
How do I draw the individual teeth? I start with an interval [lo, hi] and then use the lips to restrict the interval to [max(lo, upperlip), min(hi, lowerlip)]. If this interval is non-empty then I draw that vertical line segment.
(Also: while I was working on this I discovered some hacks in the face generator that I never took out, so I took them out. I had been trying to add more control points to make the mouth more expressive, but those extra points never worked right.)
The horizontal lines are a bit harder. It depends on whether the lips are up or down from the corners of the mouth. Case 1 is relatively easy, as a horizontal line has to be clipped once:
Case 2 is a little trickier. A horizontal line might be clipped once or split into two segments:
Case 3 is similar:
Case 4 would be the upper lip going down and the lower lip going up. This should not let you see anything inside the mouth.
I think I can handle these by finding all the intersection points on a horizontal line, and then drawing between pairs of them. I tried that, and it worked. Hooray!
So I got things working!
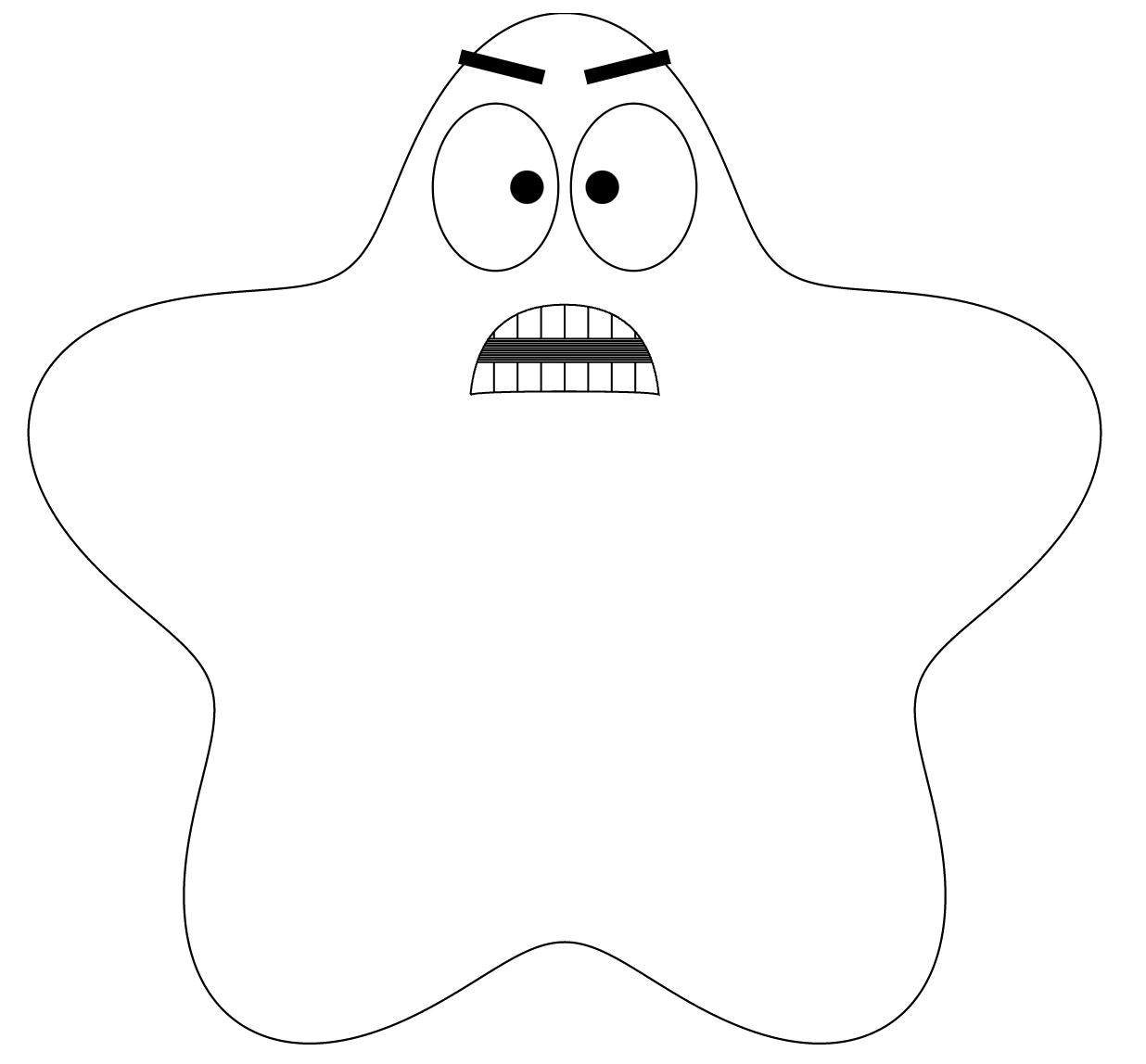
I tried reloading repeatedly with random parameters, and found a case that didn’t work:
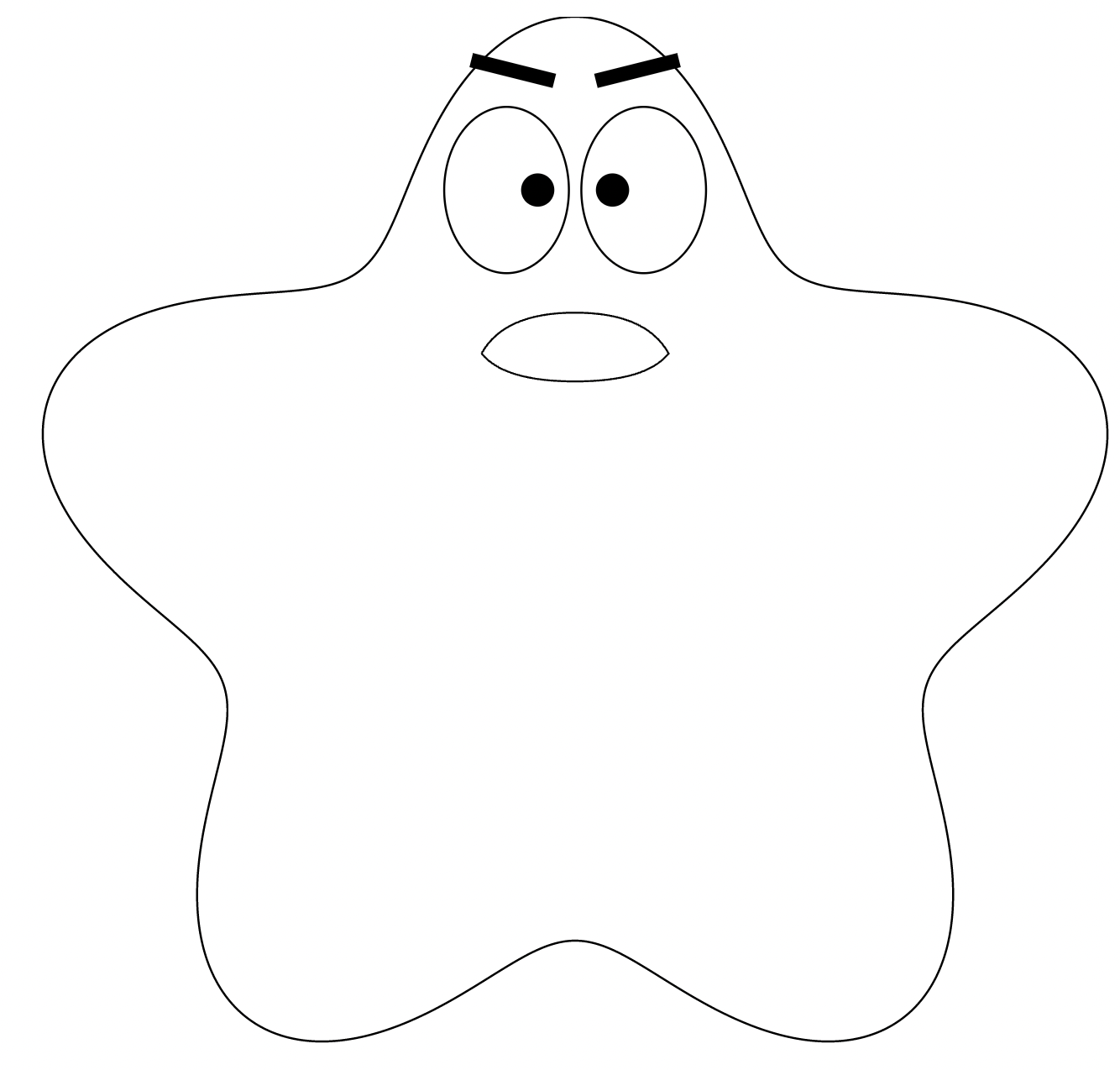
Ok, so how do I debug this? As part of generating random parameters, I printed them to the console so I knew exactly what parameter values caused it to fail, and I was able to set it to use those parameters every time:
Object.assign(FaceGenerator.shape,
{m: 0.02, p: -0.87, q: -0.62, r: 0.52, s: 0.37});
This is important for debugging! I now had a situation that failed every time I ran the program, so I could attach the debugger, add logging, add debug visualizations, etc. to investigate.
Aha, it turned out to be a problem with my parameterization. I’ve known it’s a problem, but the way I rendered it previously hid the problem so I didn’t worry about it. The parameterization of mouths is a 5-dimensional hypercube, and my goal was to have every point in that hypercube be a valid mouth. But they’re not. When m + p + q < 0 the two lips overlap and mess up the drawing. You can think of this as being one corner of the hypercube that I need to cut out. For now, I worked around the problem by pushing the lips apart if they overlap.