Note: the /x/ series of posts on my site are mostly unpolished mini posts. The polished version of this will come later, maybe in a few months.
When I think back on my polygon map generator project[1] from 2010, the word I associate most with it is voronoi. I originally used Voronoi diagrams in two places:
- I selected a nice “blue noise” distribution of points
- I constructed polygons around those points and assigned biomes
TL;DR: after writing that tutorial, I changed the demo to reshape the polygons using centroids instead of Voronoi, but I left the word “voronoi” throughout the tutorial. Oops. I finally studied this problem in May 2017 and realized what I had done:
The even distribution of points can be implemented in many ways, including poisson disc sampling[2]. The polygons were the main thing I wanted from Voronoi. I used both the Voronoi polygons and the Delaunay triangulation for different parts of the map generator. The Voronoi polygons and Delaunay triangulations are “duals” of each other. Each Voronoi polygon (white edges, blue vertices) corresponds to one red point; each Delaunay triangle (black edges, red vertices) corresponds to one blue point. I used the red points for biomes, quests, roads; I used the blue points for rivers, ridges, valleys.
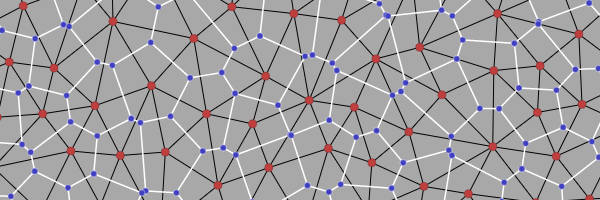
Although the parts all connect and correspond, three things were tricky to handle in the map generator:
- The blue points might not be inside the Delaunay triangles.
- Although the red (seed) points are nicely spaced, the blue points are sometimes right on top of each other. When the blue points are close to each other, the Voronoi edges are too short.
- Each Voronoi edge (white) is perpendicular to the corresponding Delaunay edge (black) but they may not actually cross.

Voronoi diagrams offer lots of nice properties. The polygons are convex. The edges are perpendicular to the Delaunay triangle edges. Any point is associated with the closest seed point. However it turns out I didn’t really need these properties for the procedural map generator. I wanted these properties:
- The red points must always be inside the polygons. The blue points must always be inside the triangles.
- The black edges must have reasonable length, so the red points will be nicely spaced out. The white edges must also have reasonable length, so the blue points will also be nicely spaced out.
- The white edges and the black edges must cross.
I was pretty happy with the Voronoi+Delaunay combination except for the locations of the blue points. Voronoi starts with the red seed points, constructs the white edges to be perpendicular to the black edges, and then places the blue points where the white edges intersect. If I moved the blue points, I could solve all three of my problems.
Voronoi places the blue points at the circumcenters[3] of the Delaunay triangles. The circumcenters and orthocenters are not guaranteed to be inside the triangles, but incenters[4] and centroids[5] always are. I constructed my own non-Voronoi polygons by placing the blue points at the centroids. The resulting polygons have the same number of vertices and edges as the Voronoi polygons, but the vertices are placed differently. On the left, polygons constructed with Voronoi; on the right, polygons constructed from the Delaunay centroids:
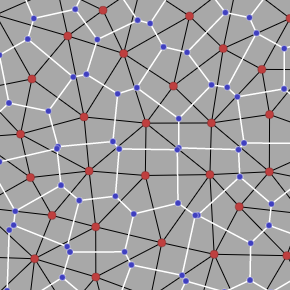
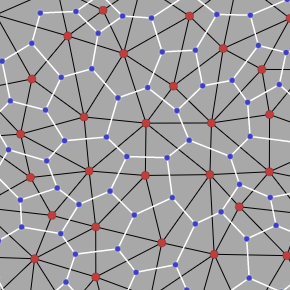
Notice in particular how every blue point is contained within its corresponding triangle, by construction. The blue points are spaced evenly. The white edges and black edges always cross, but aren’t perpendicular. I also made an animation of the comparison.
Centroid polygons aren’t without their flaws. I wasn’t sure whether the polygons would always be convex; AegisToast on Reddit shows that they are[6], but Kastenfrosch2 has an example where they aren’t[7], and even worse, Kastenfrosch2’s example shows that the red points may be outside their polygons! In trying to construct something where the blue points stay inside their triangles, I have lost the Voronoi property of keeping the red points inside their polygons. I’m not sure what to do about this.
Here’s how they look at a larger scale, with ~600 points. The voronoi-based polygons look more “boxy” whereas the centroid-based polygons look more “rounder” and “cellular”, but they have less consistent sizes:


I generated some much larger polygon networks too, using ~6000 points. Click to see the large version; I suggest loading both in separate tabs, then flipping back and forth to compare.


And then I generated even larger ones, using ~68000 points: voronoi and centroid.
I’m pretty happy with this! Delaunay centroid polygons are a better match for my procedural map generation projects. Update: [2017-08-03] It turns out I was using them all along in my 2010 map generator, but didn’t realize it. I had put in a “quick hack” to move the points around. And that quick hack turned out to be calculating exactly the same thing as the centroid. Doh! Other people[8] had figured this out at the time too.
More ideas to try: instead of always using centroids, what if we used centroids only when the circumcenter (from voronoi) falls outside the triangle (idea from FacitiusVir on reddit[9])? What if we picked a random point inside the triangle[10]?
I’m a novice at math and computational geometry, so I’m only touching the basics here. Other things I found, mostly after writing this blog post:
- After posting this blog entry, I learned that this is called the barycentric dual mesh. The primal mesh is the triangles (red dots, black lines) and the dual mesh is the polygons (blue dots, white lines). Voronoi is the circumcentric dual mesh and what I’m using is the barycenter (centroid) dual mesh. These types of meshes show up in 3d modeling and also in scientific calculations like fluid simulations.
- [2017-08-03] Also after posting this blog entry, I looked at my code from 2010 and found that I had done the very same thing back then but at the time I thought it was a hack. Now I know it’s not!
- Circle packing dual mesh[11] may have better properties than the barycentric dual mesh, but I haven’t investigated.
- HOT: Hodge-Optimized Triangulations[12] [PDF] has a nice overview in its introduction, including mentioning a hybrid between barycentric and circumcentric dual meshes. The paper proposes an even better approach that keeps both the red and blue points in good positions.
- This page[13] is about discrete exterior calculus, which is a type of calculus that works on this type of mesh.
- “Optimal Delaunay triangulations” are Delaunay triangulations with better mesh properties, either by moving vertices around, or by adding Steiner vertices[14] at “bad” points. This might let me skip the Poisson Disc step. These slides[15] have a different algorithm for picking good points based on Delaunay triangulation.
- Centroidal Voronoi tesselations[16] places the seeds for Voronoi in the center of the mass of the Voronoi polygons; I believe this is related to Lloyd’s method for constructing blue noise points.
- Triangulated irregular networks[17] are often used for map representation.
- Pitteway triangulations[18] ensures that the white edges (Voronoi) and black edges (Delaunay) cross
- Gabriel graphs[19]
- Urquhart graphs[20]
- Relative neighborhood graphs[21]
- Plateau’s Laws[22] describe the structure of soap bubbles; also see this discussion on stack exchange[23].
- Triangles have many different types of center: circumcenter, centroid, incenter, orthocenter, and more. The incenter and centroid are always inside the triangle; I tried both and found the centroid looked a little better for my use. There are at least 13240 different types of triangles centers! Clark Kimberling has been compiling a list[24].