Thin wall field of view

For my roguelike project this year I'm implementing "thin walls". The walls will be along edges instead of occupying a full tile. I had to build a new map generator to support this style of wall, and I also had to build a new field of view algorithm. I also have page about visibility with polygon obstacles.

I want to calculate which tiles are visible, with the walls blocking your vision:

I'm calculating this for one 90° sector at a time, as it simplifies the logic.

 1  Range expansion#

The main idea here is that the range will expand as we move away from the player:

This comes from "similar triangles" in geometry class. Any subrange will expand the same way:

That means we can start with the full range, then reduce it every time we see a wall:

 2  Range subtraction#

One of the main ideas I wanted to pursue was maintaining an visible set of ranges, \((a_{1}, b_{1}), (a_{2}, b_{2}), …\), where \(a_{1} ≤ x ≤ b_{1}\) OR \(a_{2} ≤ x ≤ b_{2}\) OR …. These would be the horizontal green lines in the above diagrams.

On each horizontal edge, I subtract the set of walls \((p_{1}, q_{1}), …\) from the visible set.

Then to move to the next horizontal row down, I need to widen the visible set by multiplying each value by \((y+1) / y\). For example in the above diagram, the visible range is \(-0.5 ≤ x ≤ +0.5\) at \(y = 0.5\). Then moving up a row, it expands to \(-1.5 ≤ x ≤ +1.5\) at \(y = 1.5\).

What is the algorithm for range difference?

for (let shaded in wallSet) {
    visible = visible.flatMap(lit => subtract(lit, shaded));
}

function subtract(A, B) {
    return [
        {left: A.left, right: Math.min(A.right, B.left)},
        {left: Math.max(A.left, B.right), right: A.right}
    ].filter(range => range.left < range.right);
}

Test cases and visualizations for a single segment subtracted from a single segment:

Also see https://www.ics.uci.edu/~alspaugh/cls/shr/allen.html^[1]

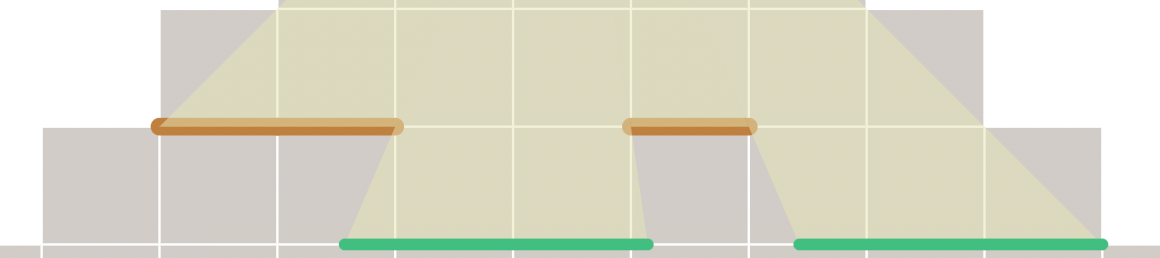
 3  Horizontal walls#

TODO: this should be fairly simple, as I already have that diagram above, but I just haven't coded up the algorithm yet

As we walk down the rows, subtract out the range of the walls from the current visible range:

 4  Vertical walls#

TODO: this is trickier

For the output, we need to evaluate the middle of each row. A vertical wall casts a shadow like this:

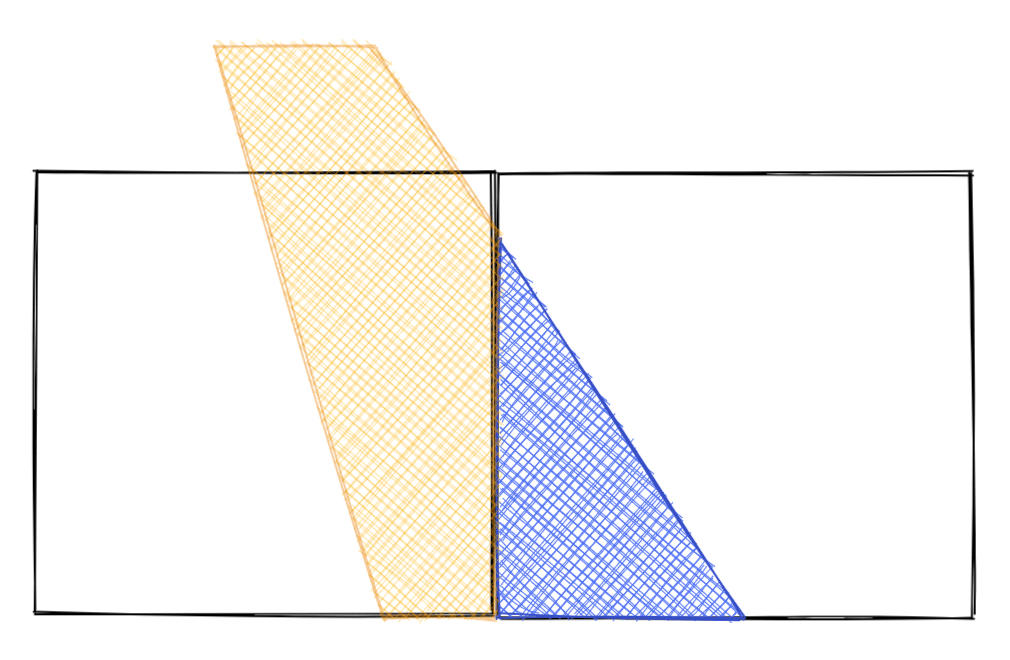
So we need to know if the shadow triggers before or after the middle of the tile. I haven't worked out the details yet.

 5  Symmetry#

TODO: Like the albertford tutorial, I will make 4 copies of this using rotation to calculate the visibility in each direction

First take a coordinate and subtract (player.x, player.y). Then rotate (dx, dy) one of four ways: (dx, dy), (dy, -dx), (-dx, -dy), (-dy, dx). Then add back (player.x, player.y). Doing this for thin walls is slightly trickier but not hard.

 6  More#

• https://gist.github.com/Slogo/2f1f1eed8231445a66c9a3aa14d31f27^[2]
• albertford page https://www.albertford.com/shadowcasting/^[3]
• roguebasin pages http://www.roguebasin.com/index.php?title=FOV_using_recursive_shadowcasting^[4]

Note that my algorithm is not recursive but seems to behave similarly to the recursive shadowcasting approaches.